Trading the curve

The basics

I received a lot of questions about curve trading. While it might once have seemed like an esoteric trade, reserved only for specialized traders (fixed income desks), with the emergence of many ETFs it has become a trade accessible to retail investors as well.

In this piece we will analyze: - what are curve trades and how to calculate them; - on what basis they move; - how to take a position based on one's own macroeconomic view.

WHAT ARE “CURVE TRADES”?

A curve trade is a trade that affects two (or more) points on the interest rate curve at the same time. In the graph above I have plotted the American 2y, 10y and 30y (respectively in white, blue and orange). In the lower panel I have therefore plotted two classic indicators of the curve:

- the 2-10 (the difference between the 2y and the 10y);

- the 2-30 (the difference between the 2y and the 30y).

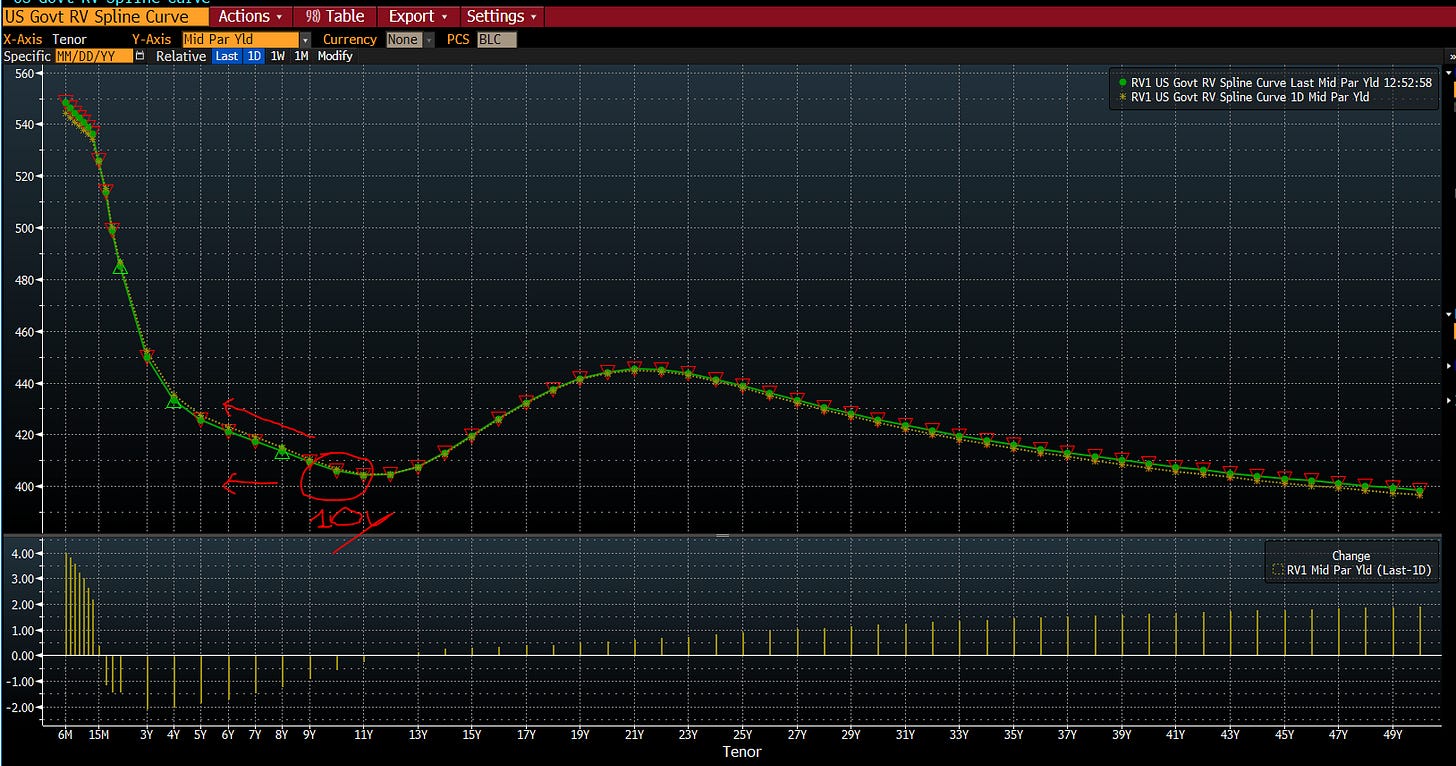
However the possibilities are endless and we can have an example below using the bloomberg HSA (Historical Spread Analysis) function.

The basic spread (just for charting purposes) is calculated simply taking the mathematical difference between the two points. For example the 2-10 below (now at -72bp) is calculated taking 4.08% (the yield on the 2y bond) less 4.81% (the yield on the 10y bond).

Returning now to the first graph (the one with the rates and curve spreads) it is possible to see very easily that: - periods in which rates fall correspond to steepening movements of the curve (short-term rates fall more than long-term rates) and we can therefore call it "bull steepening"; - periods in which rates rise correspond to flattening movements of the curve (short-term rates rise more than long-term rates) and we can therefore call it "bear flattening".

This happens because the shorter-term parts of the curve (such as the 2y) are the most sensitive to central bank actions and therefore to changes in the official rates of the FED or the ECB.

Therefore, in periods (such as the last two years we have experienced) of rate hikes, a flattening movement of the curve is usually associated, while in periods of economic slowdown (therefore with central banks returning dovish again and cutting rates) rates fall and all this is associated with steepening movements.

I intentionally wrote "usually" because this applies to medium-term movements (lasting several months or years). However on shorter time frames we can have some more complications with: - curve steepening but rates rising (bear steepening), as in the last week following the downgrade of the US rating by Fitch and the high supply of debt and budget deficit; - falling rates but a flattening curve (with longer-term parts falling faster than short-term parts (bull flattening). Below a graph taken from MSCI.

We now know how spreads are calculated and the economic basis behind it. So if, for example, we had a high conviction of an imminent recession (and therefore of a central bank that could cut rates again, our alternatives could be:

- take a directional view (and buy either the 2y, the 5y, the 10y or the 30y);

- take a steepening position (because maybe we are more uncertain about the precise timing)

But let's now look at the more technical part of curve trades (ie how they are constructed in practice) and the very important aspect (which can impact from time to time on the choice of form of trade) of the carry/roll of the position.

HOW TO BUILD A POSITION?

Curve trades, whether they are steepening or flattening (but also fly involving 3 points of the curve), are usually constructed to have limited or no directional impact. However, if then the desired curve movement (for example the steepening) takes place in bull form (with falling rates) or bear (with rising rates) it can have a huge impact on the performance of our trade.

(Chart below from Erste Asset Management)

To structure a trade that has limited directional impact the risk on the long leg of the trade must equal that on the short leg of the trade. In the fixed income world this means that the DVO1 of each leg (calculated starting from the duration of the bond or future) must be equal but of opposite sign.

Let's look at an example using Bloomberg's FIHA (Fixed income Horizon Analysis) function.

In the example I took a short position on 10y and long on 2y (hence a steepening).

Given that the duration of the 10y is 8.05 years, while that of the 2y is 1.85 years, the position on the shorter stock must be approximately 4 times larger than the position on the longer stock.

Mathematically:

- 2y: 4.35M x 1.85 years = 8 years

- 10y: 1M x 8.05 years = 8 years

CARRY/ROLL: WHY IS IMPORTANT?

Given the shape of the US yield curve, which is steeply downward sloping (with short rates much higher than long rates), taking a long 10y position can prove to be a very expensive trade if the timing is wrong. In fact, the concept to keep in mind is that: at the same interest rates (i.e. if the Fed leaves hold for long rates) in 1 year the 10-year bond will have a duration comparable to a 9-year bond (which implies that it will probably have a higher yield than which we bought it, with a related price reduction).

Making things easy, and taking 1y as a time horizon, the carry for a bond with a 2-year maturity is equal to: 1y carry for a 2y bond = 1y 1s - 2y spot (where 1y 1s is the 1y spot in 1y fwd)

while the roll down is equal to:

1y roll for a 2y bond = 2y spot - 1y spot

so putting it all together we will have

1y carry + roll down for 2y bond = 1y 1s - spot 1

The bloomberg GOVY function helps us by doing the calculations for us

Given the shape of the curve, the cost of the position is enormously penalizing (with negative returns on the whole curve). Now, using an other function (CARY - Carry and Rolldown analysis) you can compare different strategies.

There is a caveat here. This function uses the swap curve and not the government one but in the case of the US (where the swap spread is low at the moment) it is an acceptable approximation.

Both this function and the previous one (CARY) already consider the different riskiness of the different stretches of the curve, making the different points already comparable.

From this function we can see that the carry and roll of a steepening 2s10s position is equal to:

-116bp+21bp = 95bp over a 1y horizon

making the steepening position penalizing even worse than the long one on the 10y outright. A similar result also emerges using cash securities directly and the FIHA function with a negative 1y carry of -75bp.

For now I think that's all. If you liked reading it and want to support my job, please share this piece to friends and colleague and subscribe to the newsletter using the link below.

I appreciate a lot your comments but I don't want to make my piece behind a payment wall, so if you want to support me I created a page on "Pay me a coffee' https://www.buymeacoffee.com/CreditMacroMicro

Credit_Junk